【命題一】:
該文作者利用排序不等式(arrangement inequality)證明。此題似乎可以對應到高中課本習題中的一道證明題:
【命題二】:
我發現【命題一】亦可利用算術平均術大於或等於調和平均數( )的方式證明,遂拿此題問同學,結果有兩位同學分別給出不同的證法,其中之一經提示後,亦得與我雷同之證明方式,但也另外提出利用柯西不等式(Cauchy’s inequality)的證法。另一名同學使用的是算幾不等式的方法。
)的方式證明,遂拿此題問同學,結果有兩位同學分別給出不同的證法,其中之一經提示後,亦得與我雷同之證明方式,但也另外提出利用柯西不等式(Cauchy’s inequality)的證法。另一名同學使用的是算幾不等式的方法。
 )的方式證明,遂拿此題問同學,結果有兩位同學分別給出不同的證法,其中之一經提示後,亦得與我雷同之證明方式,但也另外提出利用柯西不等式(Cauchy’s inequality)的證法。另一名同學使用的是算幾不等式的方法。
)的方式證明,遂拿此題問同學,結果有兩位同學分別給出不同的證法,其中之一經提示後,亦得與我雷同之證明方式,但也另外提出利用柯西不等式(Cauchy’s inequality)的證法。另一名同學使用的是算幾不等式的方法。
由算術平均術大於或等於調和平均數,
〈證法三〉:(利用科西不等式):
由柯西不等式:
【命題三】:
證明:
移項得
即
故
證畢。□
【命題四】:
證明:
又
故
移項得
即
故
證畢。□




















































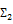












沒有留言:
張貼留言