設n為正整數,我們知道(x+1)n展開,即二項式定理的結果:
令x=1,則得
(*)
若將上式(*)展開,並提出1/n,可得
移項後得
(1)
此外,
把結論寫下來,即:
(2)
利用類似的方法,亦可得
把結論寫下來,即:
(3)
要得到上列各式的結果,亦可考慮直接函數
並對函數fn-1(x)和fn(x)的這兩種表示法分別作積分及微分,即得:
故得
即第(1)式的結果。
故
令x=1,即得第(2)式的結果
同理,把fn(x)微分兩次,即得
故
令x=1,即得第(3)式的結果

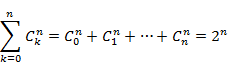




























沒有留言:
張貼留言