這是最近看到的一道題,出處是國立清水高中98學年的教甄考題,我覺得蠻有趣的,實際上我也花了一點時間思考。不知道還有沒有其他的解法?
因此,
由上討論雖然可以算出 的值,那要怎麼判斷個位數字呢?我們利用遞迴關係式。實際上
的值,那要怎麼判斷個位數字呢?我們利用遞迴關係式。實際上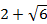 和
和 是x2-4x-2=0的根,此方程式即遞迴關係式 an+2=4an+1+2an 的特徵方程式,若這個遞迴式的第n項為
是x2-4x-2=0的根,此方程式即遞迴關係式 an+2=4an+1+2an 的特徵方程式,若這個遞迴式的第n項為 ,將n=0和1代入,即得a0=2,a1=4。所以我們可以寫出
,將n=0和1代入,即得a0=2,a1=4。所以我們可以寫出
 的值,那要怎麼判斷個位數字呢?我們利用遞迴關係式。實際上
的值,那要怎麼判斷個位數字呢?我們利用遞迴關係式。實際上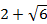 和
和 是x2-4x-2=0的根,此方程式即遞迴關係式 an+2=4an+1+2an 的特徵方程式,若這個遞迴式的第n項為
是x2-4x-2=0的根,此方程式即遞迴關係式 an+2=4an+1+2an 的特徵方程式,若這個遞迴式的第n項為 ,將n=0和1代入,即得a0=2,a1=4。所以我們可以寫出
,將n=0和1代入,即得a0=2,a1=4。所以我們可以寫出












沒有留言:
張貼留言