斐波那契數的矩陣表示法及兩個相關公式

斐波那契數列(Fibonacci Sequence)的遞迴式是f₀=0，f₁=1，f_k+1=f­_k+f_k-1，其中k為任意的自然數。可以利用

(1)                      

的關係，以及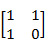的特徵值(eigenvalues)為、，以及相對應的特徵向量(eigenvectors)分別為、，得到

                   

 ，對應(1)的矩陣中的元，即可得

。

(以上的內容，亦可參考前一篇：The general term of the Fibonacci Sequence)

 利用(1)，取行列式值，即可得

(2)                                                              。

 同樣由(1)，取k=m+n，因為

計算矩陣的第(2,2)的元，可以得到

(3)                                                            。

當然，也可以利用數學歸納法得到(2)和(3)的結果。

觀察下面的圖形，其中∠B為直角，，的長度分別為f_2n、f_2n+1、f_2n+2，很容易推得的長度分別為f_2n-1和f_2n+1。

取(2)中的k=2n，移項後得f_2n-1f_2n+1＝1+ f_2n ²，即，若且唯若，故由SAS相似性質知，三角形ACD～三角形ECA，故∠CAD＝∠AEC＝α，所以三角形ACD的外角θ＝α+β，即 

。