【題】設
 為一圓的直徑,A1、A2、…、An為圓上的點,對於所有的i=1~n,作
為一圓的直徑,A1、A2、…、An為圓上的點,對於所有的i=1~n,作 ,其中Di為垂足,若
,其中Di為垂足,若 ,試證:
,試證: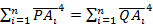
Pf:
對於所有的i=1~n,因為Ai在圓上,所以∠PAiQ=90°,故 ,且由母子相似性質知,
,且由母子相似性質知, ,
, ,及已知條件
,及已知條件 ,可得
,可得由於
 ,i=1~n,所以
,i=1~n,所以 。故
。故
其實命題時上面這個題目的想法是從猜拳輸、贏的平方和與標準差出來的,簡單對照一下,就可以發現它的關聯了。
【題】設三角形ABC的邊長分別為a、b、c,外接圓半徑長為R,內切圓半徑長為r,三角形DEF的三邊長分別為a+b、b+c、c+a,試求三角形DEF的內切圓半徑長。
Sol:








