還有一些題目在<
交點個數、分割的區域個數的遞迴關係式>這一篇裡。
再來幾道常見的題目,我們只寫出遞迴關係式,不去求它的一般項。
1.
某人寫了n封信給n個人,放入已寫好收件人的信封裡,若隨意放入,則全部放錯信封的情況有an種。
設信與信封正確的配對方法為(L1, E1)、(L2, E2)、…、(Ln, En)。
若是全部放錯信封,假設放法為(Ln, Ek),k≠n,我們可以考慮放到信封En的信,有兩種情況:
一為(Lk, En),即Lk和Ln放錯的信封剛好相反,因為其他的(n-2)封信也放錯信封,所以有an-2種放錯的情況。
另一種情況為(Li, En),其中i≠k、n,即放到信封En的信不是Ln,也不是Lk,如果我們把Li放到Ek(仍是錯放),把Ln放回En(或直接抽掉Ln和En),這動作並不影響其他信與信封的放置情況,所以有an-1種情形。
因此若是(Ln, Ek),方法數為an-1+an-2,又k可為1~n-1,所以an=(n-1)( an-1+an-2),邊界條件為a1=0,a2=1。
如果用來處理n的值較小的情況,例如,有7封信卻全部放錯信封的情況,我們只要列出〈an〉: 0, 1, 2, 9, 44, 265,
1854, …,所以共有1854種錯放的情形。
2.
如圖,有n個相鄰空格x1, x2,
…, xn,用m種顏色著色,m>1,一格只能塗一色,且相鄰不同色,則塗法有an種。
若依序從x1,x2開始著色,最後一個塗的空格是xn,針對塗上xn的顏色的方式,我們可以分成兩種情況來討論:
第一,若x1和xn-1的顏色不同,則xn只能選擇異於x1和xn-1上的顏色,即xn有m-2個顏色的選擇。至於x1到xn-1的著色方法數,可以想成把xn這一格拿掉,讓x1和xn-1相鄰,因為x1和xn-1的顏色不同,所以方法數有an-1種。故此種情況的方法數為(m-2) an-1。
第二,若x1和xn-1的顏色相同,則xn就有m-1種顏色的選擇。而x1到xn-1的著色方法數,可以想成將xn這一格拿掉,因為x1和xn-1的顏色相同,所以讓x1和xn-1接合成同一格,這樣的著色方法數就有an-2種。故此種情況的方法數為(m-1) an-2。
綜合以上兩種情況,可得an=(m-2) an-1+(m-1) an-2,n≧4;邊界條件為a1=m,a2=m(m-1),a3=m(m-1)(m-2)。
3.
擲一枚硬幣,若出現正面的機率為p,出現反面的機率為q=1-p,若投擲n次,則不出現連續2次正面的機率為an。
考慮第n次擲出的情形:
若第n次為反面,則前n-1次必須不連續出現2次正面,因此機率為qan-1。
若第n次為正面,則第n-1次必為反面,且前n-2次也必須不連續出現2次正面,因此機率為pqan-2。
綜合以上兩種情況,可得an=qan-1+pqan-2,邊界條件為a1=1,a2=1-p2。
如果這枚硬幣是公正的,即每次投擲時,出現正、反面的機率為p=q=1/2。
4.
上樓梯的方式可以一次走一階,或一次走兩階,則走n階樓梯的方法數為an。
因為一次可以走一階或兩階,因此踏到第n階的方式可以從第n-1階走一階上來,或是從第n-2階走兩階上來,前一種情形的方法數相當於走到第n-1階的方法數an-1,後一種情形的方法數相當於走到第n-2階的方法數an-2,故走到第n階的方法數為an=an-1+an-2,邊界條件為a1=1,a2=2。
這一個遞廻關係式與斐波那契數列(Fibonacci sequence)〈fn〉的遞迴式很像,只差在邊界條件,實際上,fn=an-1。因此我們可以利用這個走樓梯的方式,得出一個斐波那契數列的公式:fn+1=fk fn-k+fk+1 fn-k+1。
原因是:若要走到第n階樓梯,但第k階樓梯不能踩上去,則方法數相當於先走到第k-1階,然後一次跨兩階到第k-2階,再從第k-2階走到第n階,則方法數為ak-1
an-(k+1)=fk
fn-k。另一種想法則是走到第n階的所有方法數,減掉一定要走到第k階的方法數,即an-akan-k=fn+1-fk+1
fn-k+1。故得到fk
fn-k=fn+1-fk+1
fn-k+1,移項即得fn+1=fk
fn-k+fk+1
fn-k+1。可參考斐波那契數的矩陣表示法及兩個相關公式這一篇的第(3)式。
 的值,那要怎麼判斷個位數字呢?我們利用遞迴關係式。實際上
的值,那要怎麼判斷個位數字呢?我們利用遞迴關係式。實際上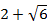 和
和 是x2-4x-2=0的根,此方程式即遞迴關係式 an+2=4an+1+2an 的特徵方程式,若這個遞迴式的第n項為
是x2-4x-2=0的根,此方程式即遞迴關係式 an+2=4an+1+2an 的特徵方程式,若這個遞迴式的第n項為 ,將n=0和1代入,即得a0=2,a1=4。所以我們可以寫出
,將n=0和1代入,即得a0=2,a1=4。所以我們可以寫出 的值,那要怎麼判斷個位數字呢?我們利用遞迴關係式。實際上
的值,那要怎麼判斷個位數字呢?我們利用遞迴關係式。實際上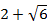 和
和 是x2-4x-2=0的根,此方程式即遞迴關係式 an+2=4an+1+2an 的特徵方程式,若這個遞迴式的第n項為
是x2-4x-2=0的根,此方程式即遞迴關係式 an+2=4an+1+2an 的特徵方程式,若這個遞迴式的第n項為 ,將n=0和1代入,即得a0=2,a1=4。所以我們可以寫出
,將n=0和1代入,即得a0=2,a1=4。所以我們可以寫出












